Robust MPC
Summary
Building an approximate model that describes certain phenomena or systems is a common practice. Apart from other characteristics, two models representing a particular system can differ on how accurate they are and how much computation they require. Ideally, we would want to have a very accurate model that also requires less computation to run. In practice, however, modeling real-world systems requires complex non-linear relationships requiring much computation. Instead, if we use simple tractable models such as a linear model, we gain efficiency at the cost of an accurate model approximation.
Model predictive control (MPC) is a popular algorithm for constrained control tasks. It is a standard due to the robustness of the control solution that it provides and the simplicity of the solution. The MPC formulation is based on a model of the system which we are trying to control. Due to this feature, model approximation errors can make their way into the control solution calculated by the MPC.
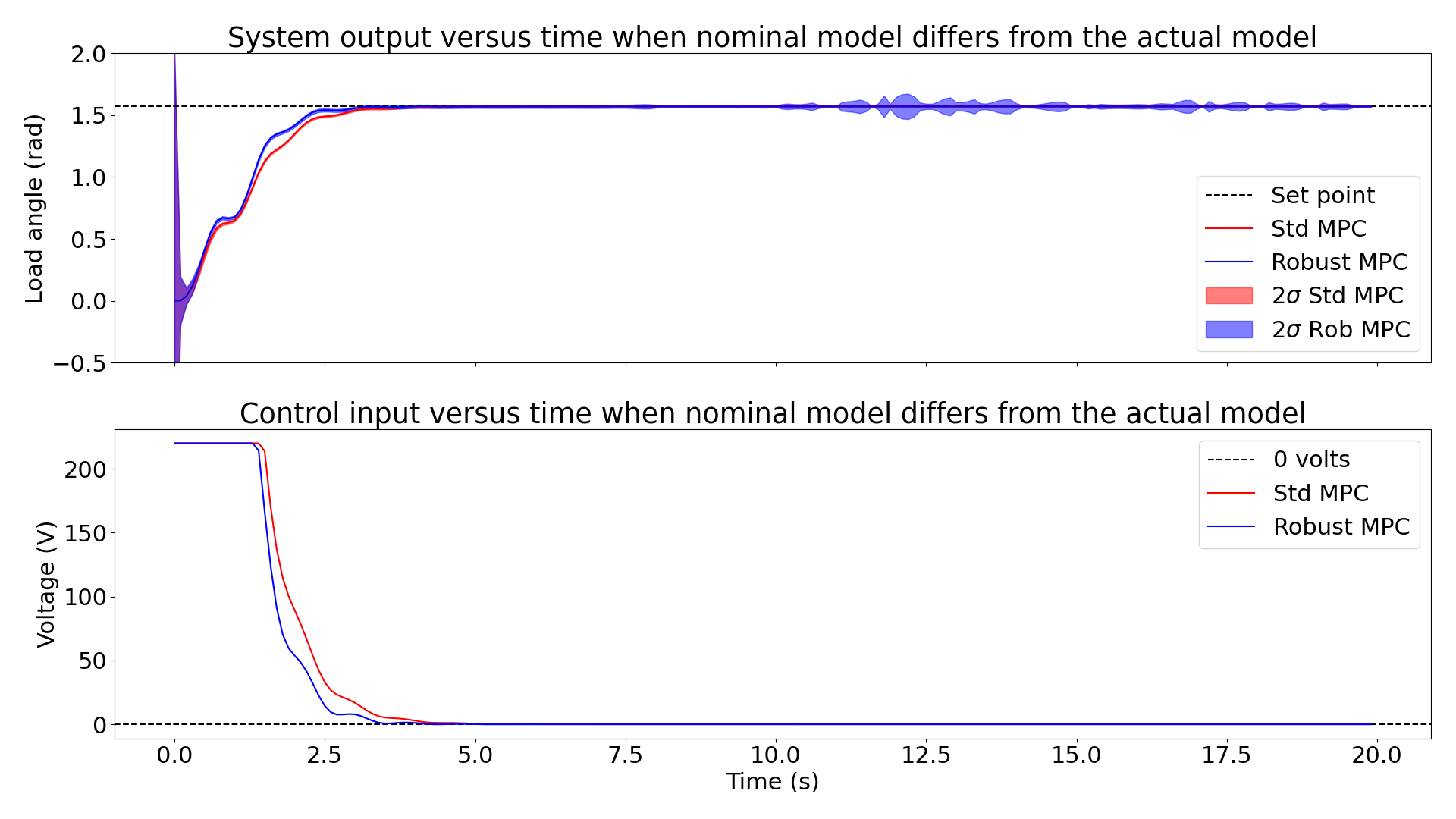
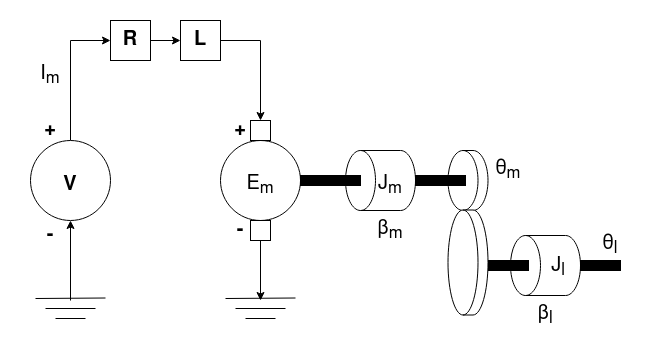
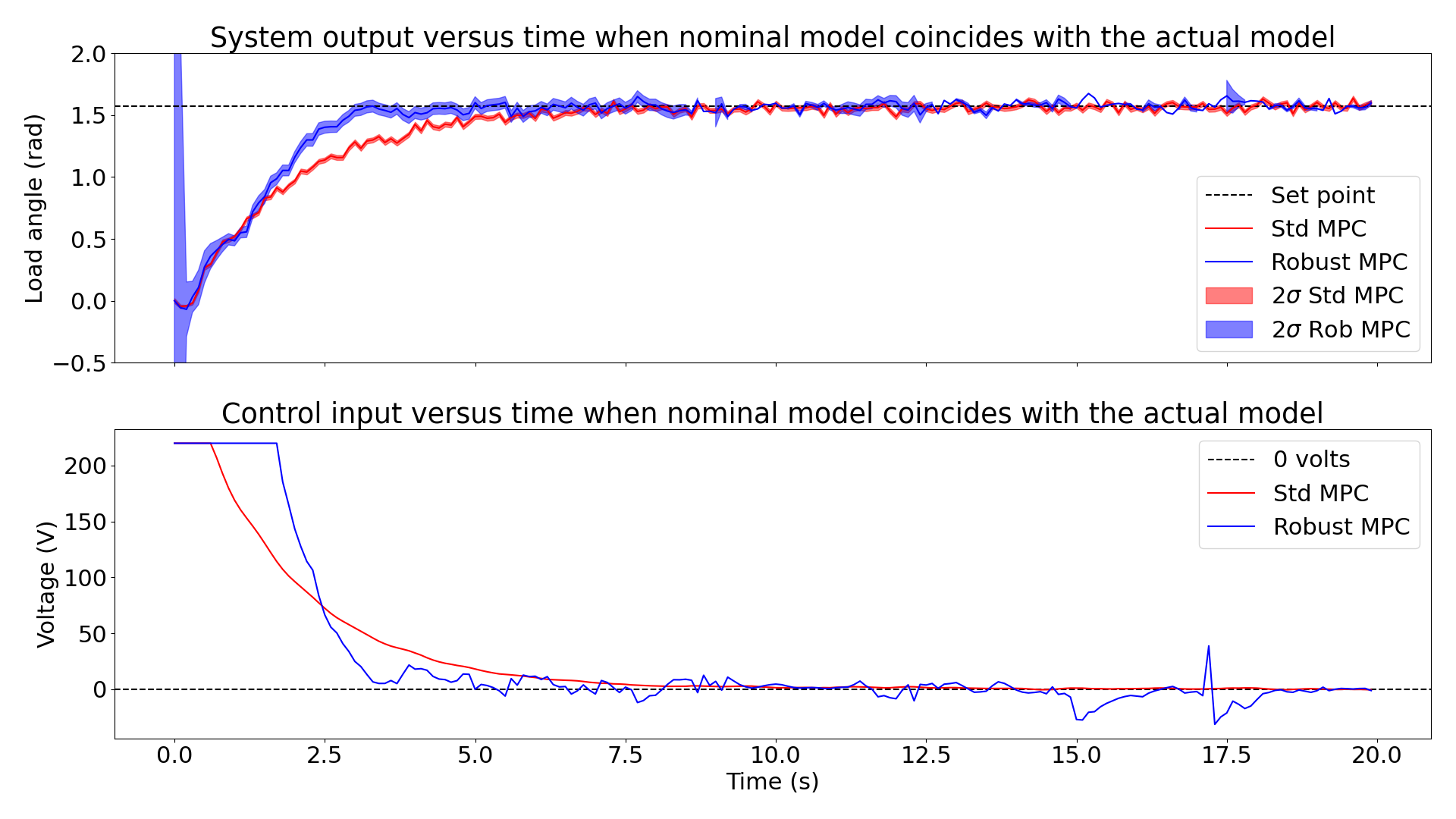
In this project, I studied and implemented a more robust state estimator for an unconstrained MPC framework (the same methodology can also be applied to the constrained MPC) that considers the possibility that the model we are working with only approximates the system. In my experiments, I compared the performance of the standard MPC formulation with a robust variant, which uses a robust Kalman filter for its state estimation. This robust variant of the Kalman filter solves a minimax optimization problem over a set of possible models contained in a ball around the approximated linear model. The robust Kalman filter considers uncertainty in model knowledge and bases its state estimate on this. To compare their performance, I applied them to a set-point tracking problem, where the load angle of the servo-mechanical system is made to track a set-point trajectory. The servo-mechanical system's dynamics are non-linear and approximated to a linear model. I performed two experiments: the first was in the scenario that the actual complex model of the system (actual model) is the same as the simple approximated linear model (nominal model), and the second was in the scenario that these models disagreed. The reader can find graphs showing the performance of both controllers in these two experiments below.
From my experiments and observations, I concluded that the robust MPC variant does outperform the standard variant by a small margin but at a higher cost. A definitive conclusion regarding the superiority of the robust MPC variant can be obtained by performing a more rigorous analysis of its performance on many different systems of differing non-linearity and a number of different control problems.
This project was initially implemented in Python for a quick development and testing process. A C++ implementation was also created at a later stage to allow for deployment on embedded devices for real-time operation of the robust MPC to control a non-linear system. The C++ implementation is about 3 - 5 times faster than the Python implementation.
Useful links
- GitHub Repository of the Python implementation
- GitHub Repository of the C++ implementation
- Project Report
Gallery
My presentation on this topic
-
Plots of the output (load angle) and input (input voltage) as a function of time when the actual model and nominal model agree
-
Plots of the output (load angle) and input (input voltage) as a function of time when the actual model and nominal model do not agree